1. Introduction
Accurate sensing of the external load at the end-effector of a manipulator has become increasingly important as robots are required to perform the tasks involving contact with the environment. Service robots, which have drawn a lot of attention in recent years, especially need such load sensing capability in order to assist humans in various tasks. 1,2 Since expensive force/torque transducers are not suitable in service robots for economic reasons, load sensing should be conducted by means of relatively cheap load sensors.
Various techniques have been used to measure the external load applied to the robot arm. Six-axis force/torque transducers-or joint torque transducers are popular among these techniques. The six-axis force/torque transducer, which is frequently mounted at the wrist of a manipulator, can accurately sense the external load acting on the robot hand. However, its structure is very complicated for accurate sensing, and thus it is too expensive to be used in service robots. Therefore, joint torque transducers are usually adopted in the practical manipulators.

The joint torque transducers require calibration for accurate sensing, where typical calibration methods include the compliance matrix computed by the structural analysis, "the least-squares method" and 7,8 the approach based on the motion of a robot arm, etc. However, the crosstalk error caused by the load components other than the target load (either force or torque) of the sensor cannot be compensated for by these calibration methods. Although the calibration method based on a neural network can cope with this problem, it cannot be applied to joint torque transducers. Therefore, most torque transducers have been designed so that the crosstalk is minimized by the structural consideration, 10-13 as shown in Fig. 1. In most cases, however, such crosstalk problems cannot be avoided due to both the manufacturing tolerances and the misalignment in strain gauge bonding.
To cope with this problem, a new calibration method consisting of the primary and secondary calibration schemes is proposed in this research. The joint torques can be obtained through the primary calibration from the torque transducer outputs, but these joint torques contain the crosstalk interference. Then, a virtual load acting on each joint torque transducer is estimated from the torque transducer output and manipulator configuration. This virtual load contains the components which cause the crosstalk interference. Then, the desired joint torque, which is free of crosstalk, can be obtained by the secondary calibration scheme. Once the primary and secondary calibration matrices are obtained off-line, an estimation of the desired joint torque, and thus the external load under consideration, can be conducted in real-time.
The main contribution of this proposed calibration method is that the relatively cheap load sensors or the custom designed sensors, which have a simple structure and relatively low accuracy, can be used for accurate sensing of the external load.
The rest of this paper is organized as follows. The concept of the crosstalk error related to the joint torque transducers is presented in section II. The proposed calibration method using the virtual load is detailed in section III and the experimental verification of the proposed scheme is discussed in section 3.
2. Sensor Calibration Using Virtual Load
The crosstalk error of a load sensor discussed in the previous section cannot be compensated by means of general calibration methods. The novel calibration method minimizing this crosstalk is proposed in this section.
Overall calibration process
In this research, the new calibration method consisting of the primary and secondary calibration is proposed to cope with the crosstalk problem. The overall process of the proposed calibration scheme is illustrated in Fig. 2. The shaded box (usual process) is the real-time process for sensing of the external load, and the transparent box represents the calibration process. Each of these boxes was already detailed in the previous sections.

3. Experiments
3.1 Experimental setup
To verify the validity of the proposed calibration method, a 3DOF wrist composed of the roll, pitch, and yaw joints were constructed, as shown in Fig. 3. Each sensing frame was designed so that the strain gauges were properly bonded, as shown in Fig. 4.

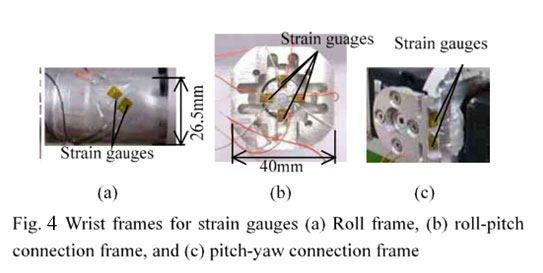
The torque T is measured by the roll frame sensor, the torques, t3 and the force Fr by the sensors installed at the roll-pitch connection frame and finally the torques T4, Ts by the sensors at the pitch-yaw connection frame. For the calibration based on the static force, the weight (500g) is installed at the end of the wrist, as shown in Fig. 5.

Note that although the virtual load vector can be calculated for each torque transducer, the identical virtual load vector can be used for the torque transducers which are installed in the same rigid frame.
3.2 Experimental results
In this experiment, a weight of 500g is attached to the end-effector to obtain sample data for calibration. A total of 200 sample data (the sensor outputs and joint angles) were collected for various configurations of the manipulator.
| Roll axis angle | 0° | 60° | 120° | 180° | 240° | 300° |
| Premary calibration | 3.75 | 4.52 | 5.12 | 5.71 | 5.28 | 4.45 |
| Error (%) | 27.9 | 7.7 | 4.5 | 21.4 | 9.7 | 9.1 |
| Secondary calibration | 4.54 | 4.89 | 5.05 | 4.70 | 4.99 | 5.30 |
| Error (%) | 7.3 | 0.2 | 3.1 | 4.1 | 1.8 | 8.1 |
A comparison of the external force after the primary calibration with that after the secondary calibration is shown in Table 1 and Fig. 6. For this comparison, a weight of 4.9N was applied to the origin of link frame 5 pointing downward, meaning the gripper grasped the weight. When only the primary calibration was conducted without the crosstalk compensation, the maximum sensor error reached 28%. However, after the secondary calibration, the maximum sensor error was significantly reduced to 8% since the crosstalk errors were minimized.

4. Conclusion
In this research, a new calibration scheme composed of both primary and secondary calibration processes was proposed to cope with the problem of crosstalk. Using the primary calibration matrix, the virtual load acting on each torque transducer can be computed. This virtual load contains the components which cause the crosstalk error. Then the desired joint torque, which is free of the crosstalk error, can be obtained by the secondary calibration, which is computed from the virtual load.
Using the proposed calibration method, the error in the load sensing was significantly reduced, which means that relatively low- quality load sensors can be reliably used to accurately measure the external load applied at the end-effector of a manipulator.
ACKNOWLEDGEMENT This work was supported by the Center for Autonomous Intelligent Manipulation under Human Resources Development Program for Robot Specialists (Ministry of Knowledge Economy).